1. 介绍
什么是数据挖掘:抽取 interesting pattern
数据挖掘的过程:knowledge discovery 过程 KDD
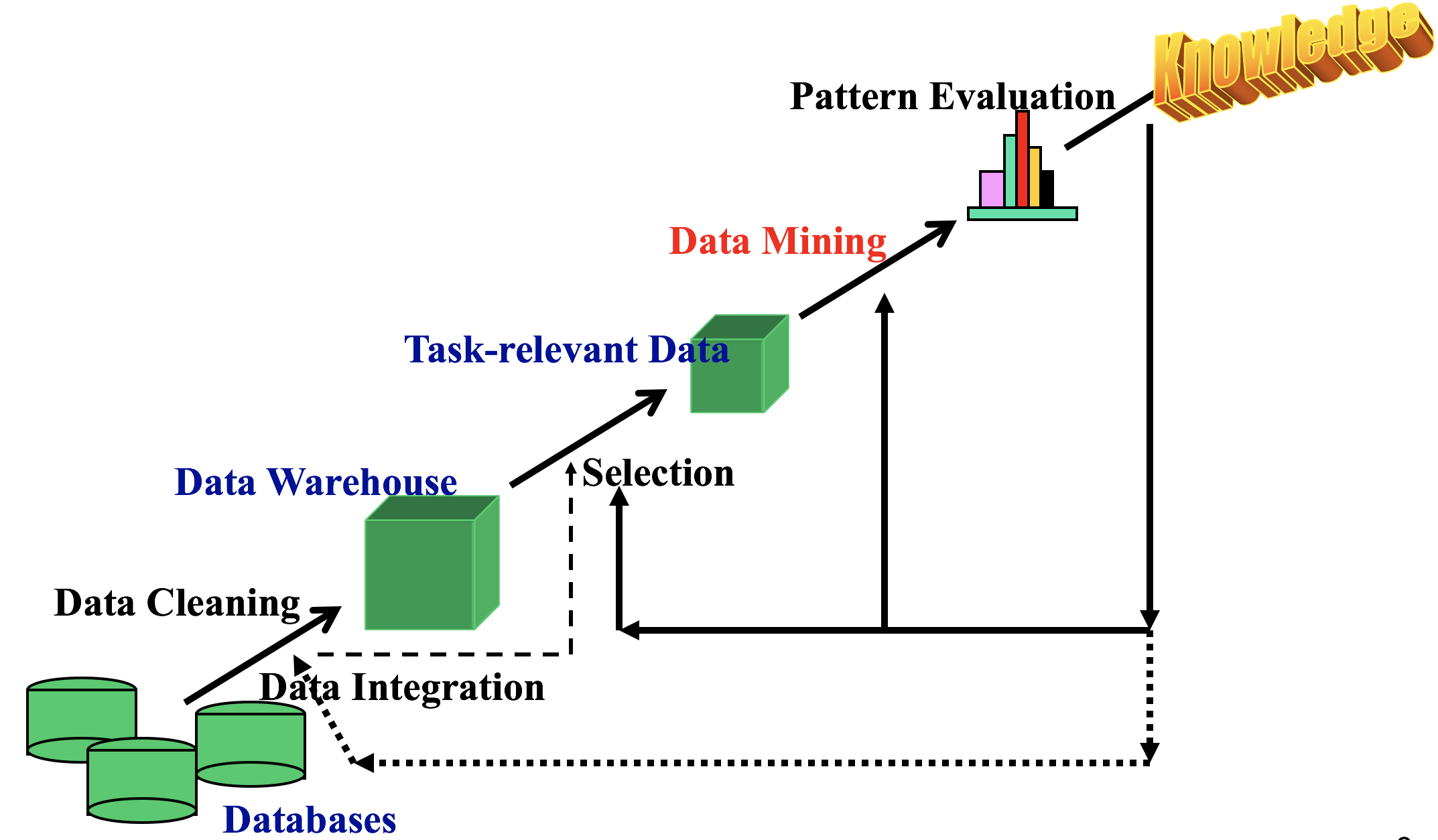
可以被挖掘的 pattern
generalization(概括)
- Information integration 信息聚合,数据仓库的构建(数据清洗、变换、聚合和多维数据模型)
- Data cube technology 数据立方技术
- Multidimensional concept description 多维概念描述(分类和识别)
association and correlation analysis(关联分析和相关分析)
- 发掘 Frequent pattern
- association correlation vs causality(关联,相关和因果关系)
classification(分类)
- 建立基于训练样本的模型
- 描述,区分不同的类别
- 预测一些未知的类别标记
cluster analysis(聚类)
- 无监督学习(比如:不知道类别标签)
- 将结果进行分类成不同的类别
- 原则:最大化类内的相似度,并且最小化类间相似度
outlier analysis(离群点分析)
- outlier(离群点):指的是不符合数据一般表现的数据个体
- 噪音?异常?
- 方法:聚类、回归分析
Time and Ordering: Sequential Pattern, Trend and Evolution Analysis(时序数据,趋势分析和演变分析)
- Sequence, trend and evolution analysis(序列,趋势和演化分析)
- 挖掘数据流
Structure and Network Analysis(结构分析和网络分析)
- graph mining:图数据挖掘
- web mining:网络数据挖掘
- 信息网络分析
数据挖掘的主要问题
- 挖掘方法
- 挖掘多种不同的知识
- 在多维空间中挖掘知识
- 跨学科
- 提高在网络环境中挖掘数据的能力
- 噪声、不确定性、数据的不完整性
- pattern 演变
- 有约束条件的挖掘
- 用户交互(和领域背景知识的结合)
- 可视化(Efficiency and Scalability 高效、可扩展)
- 数据类型的多变性
- 数据挖掘与社会影响
2. 数据
数据对象和属性类型
- 数据集的类型
- 记录(record):关系记录,矩阵,文档数据,交易数据
- 图和网络(graph and network)
- 有序数据(ordered):视频、时序数据、基因序列数据
- 空间、图像和多媒体
- 结构化数据的重要特征:
- 维度(dimensionality)
- 稀疏度(sparsity)
- 分辨率(resolution)
- 分布(distribution)
- 数据对象
- 一个数据对象代表一个实体
- 也被叫做 samples, examples, instances, data points, objects, tuples
- 数据对象用属性来表述
- rows:数据对象;columns:属性
- 属性(Attribute or dimensions, features, variables)
- nominal:枚举属性(类别数据),类别,状态,是可数的,比如 Hair_color = {auburn, black, blond, brown, grey, red, white}
- ordinal:序数属性(有序数据),属性值有一个有意义的顺序,但相邻两级之间的差距是未知的
- binary:二元属性
- 对称二元属性(等价,同权,比如男女)
- 非对称二元属性(不等价,如艾滋病毒的阴性和阳性,将重要的(往往是稀有的)编码为 1)
- numeric:数值属性
- 数值(quantity)
- 区间属性(interval):用相等的单位尺度的单元来表示,而且值是有序的。没有绝对的零值,并没有倍数关系(比如不能说 10℃ 是 5℃ 的两倍温暖)
- 比率属性(ratio):有零值
数据的基本统计描述
中位数,最大值,最小值,分位数,离群值,方差等等(median, max, min, quantiles, outliers, variance, etc.)
- mean,均值(代数意义上的)
- mode,众数,可能有多个众数
- median,中位数
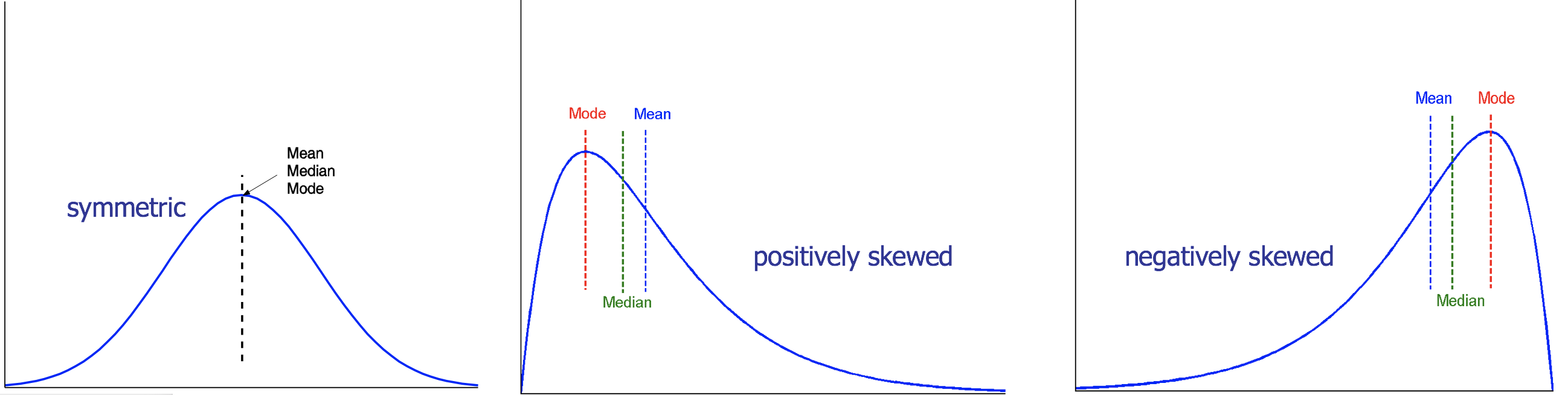
对称的和倾斜的数据:对称,正倾斜(众数小于中位数),负倾斜(众数大于中位数)
分位数,离群值和盒须图
- 分位数(Quartiles):Q1(25 分位数),Q3(75 分位数)
- 四分位数间距(inter-quartile range),IQR=Q3-Q1
- 盒须图的五个点:min, Q1, median, Q3, max
方差和标准差
有偏估计方差
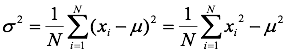
无偏估计方差
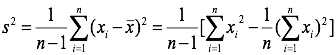
可视化
盒须图
统计直方图
分位数图(Quantile Plot),横轴是百分比,纵轴是数值
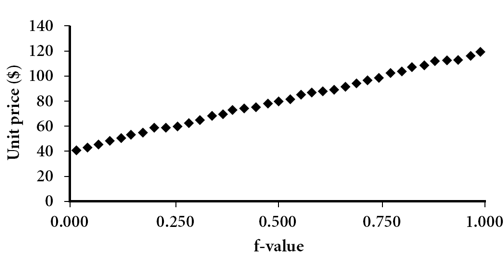
Q-Q Plot,比较两组数据是否来自同一分布
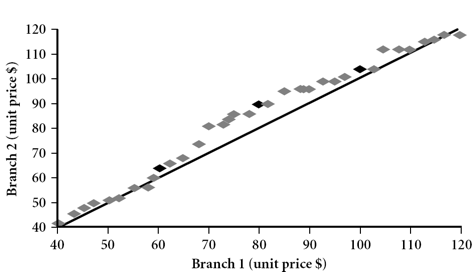
散点图(Scatter plot)
数据相似度和相异度
数据矩阵:n*p 矩阵,n 是数据对象个数,p 是属性个数。
相异度矩阵:n*n 矩阵
枚举属性(nominal attribute)的相异度度量:
- 简单的匹配,相异度 d(i,j)=(p-m)/p,p 是属性个数,m 是匹配的属性
- 将枚举属性转换成二元属性(比如 color={red, green, blue},可以转换成三个二元属性),用二元属性的相异度度量
二元属性(binary attribute)的相异度度量:
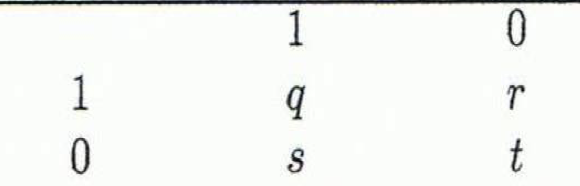
- 对称属性的距离:$d=(r+s)/(q+r+s+t)$
- 非对称属性的距离:$d=(r+s)/(q+r+s)$
- Jaccard 相关系数(非对称属性的相似度度量):$sim=(q)/(q+r+s)$
数值属性(numeric):
标准化:
Z-score: $z=(x-\mu)/\sigma$,$\mu$是平均值,$\sigma$是标准差
平均绝对离差(mean absolute deviation):计算每个属性的平均值,以及每个属性的标准差,再进行 z-score 标准化,更鲁棒
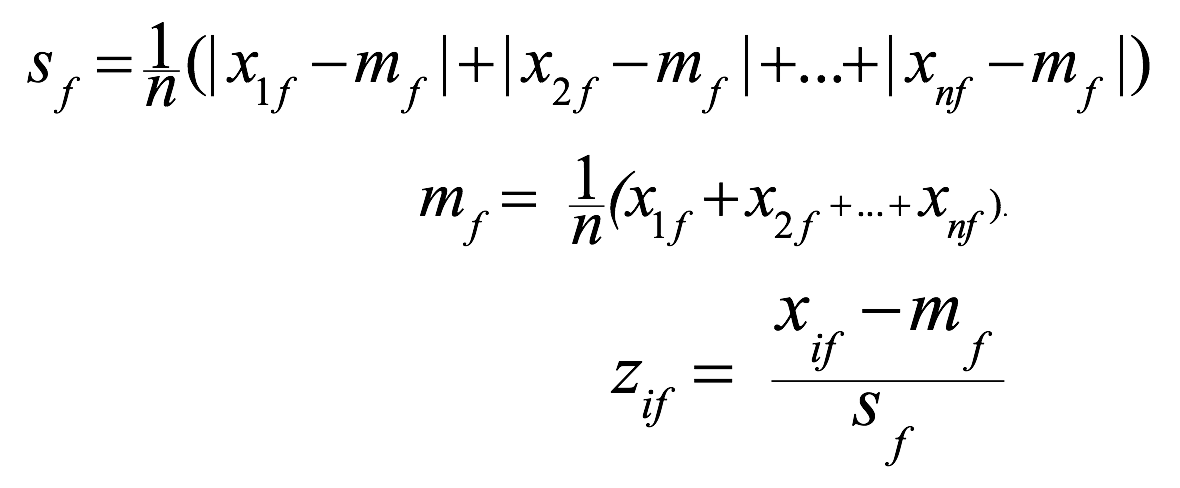
欧几里得距离(Euclidean Distance):$d=\sqrt{(x_{i1}-x_{j1})^2+(x_{i2}-x_{j2})^2+…+(x_{ip}-x_{jp})^2}$
曼哈顿距离$d=|x_{i1}-x_{j1}|+|x_{i2}-x_{j2}|+…+|x_{ip}-x_{jp}|$
闵可夫斯基距离(Minkowski distance):$d=\sqrt[h]{|x_{i1}-x_{j1}|^h+|x_{i2}-x_{j2}|^h+…+|x_{ip}-x_{jp}|^h}$
范数
上确界距离($L_{max}$,切比雪夫距离)
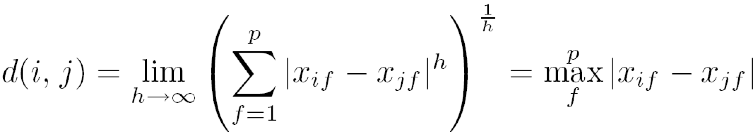
有序属性(ordinal)
标准化,映射到[0,1],$r_{if}$是原始值的排序值,$M_f$是属性$f$的状态数
$z_{if}=\frac{r_{if}-1}{M_{f}-1}$
用数值属性提到的四种距离来计算
混合类型
将所有属性,映射到共同的区间[0,1]
计算距离:

- 指示符$\delta_{ij}=0$ 表示,对象 i 或对象 j 缺少属性 f,或者$x_{if} = x_{jf} = 0$且 f 是非对称的二元属性;否则为 1。
- $d_{ij}^{(f)}$,表示 i 和 j 在属性 f 上的距离:
- 二元属性或者枚举属性:相同为 0,不同为 1;
- 有序属性,用有序属性标准化的方式进行标准化
- 数值属性,两者的差/(属性 f 的最大值-属性 f 的最小值)
余弦相似度(Cosine Similarity),一般用于计算文档,每个文档都有一个词频向量。
cos(d1, d2) = (d1· d2) /||d1|| ||d2|| ,两个向量之间的余弦值,||x||是 x 的欧几里得范式
3. 数据处理
数据质量
- 准确性(accuracy)
- 完备性(completeness)
- 一致性(consistency),有些修改了,有些没修改
- 时效性(timeliness)
- 可信性(believability)
- 可解释性(interpretability)
数据处理的主要任务
- 数据清洗(datac cleaning):填补缺失值,平滑噪声,去除异常值,解决不一致性
- 数据集成(data integration):将多源数据进行集成
- 数据简化(data reduction):降维、数量归约(使用回归,聚类等方法,用较小的表示取代数据)、数据压缩
- 数据变换和离散化(Data transformation and data discretization),进行标准化
数据清洗
- 缺失值
- 忽略
- 手动
- 添加为新的类别,比如 unknown
- 用平均值或者中位数来填充
- 用同一类的样本的均值或者中位数来填充
- 最有可能的值:贝叶斯形式化方法(Bayesian formula)或者决策树
- 噪声
- 分箱,划分成等频率的箱,用箱的均值或者中位数,或者最近边界来平滑数据
- 回归
- 聚类:检测并去除离群值
- 人机合作
- 不一致性(如何检测?)
- 用元数据(定义域,值域,分布等)
- 字段过载(field overloading),用了其他属性的未使用的部分的位置
- 检查唯一性规则(每个值都应该不同),连续性规则(最低和最高之间没有确缺失值),空值规则
- 使用商业工具
- 伪造
数据集成
多源数据的结合:模式集成(schema integration, e.g. nA.cust-id = B.cust-#),个体识别(entity identification,识别有不同名称的相同的个体),检测和解决数据值冲突。
数据集成中的冗余(redundancy)问题
两种冗余:同一个属性或者对象有着不同的名称;可被推导出来的值
可以通过相关分析(correlation analysis)和协方差分析(covariance analysis)进行冗余检测
相关分析:$\chi^2$卡方检验
$\chi^2=\sum\frac{(Observed-Expected)^2}{Expected}$
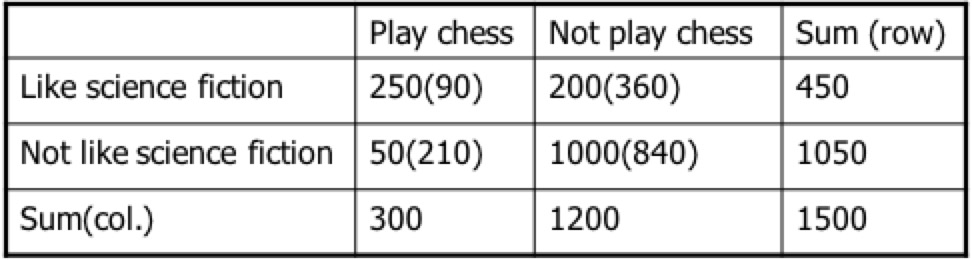
括号中的是它的期望值,比如,90=450*300/(300+1200),于是
$\chi^2=\frac{(250-90)^2}{90}+\frac{(50-120)^2}{210}+\frac{(200-360)^2}{360}+\frac{(1000-840)^2}{840}$
卡方越大越相关。
相关分析:皮艾森系数(Pearson’s product moment coefficient)
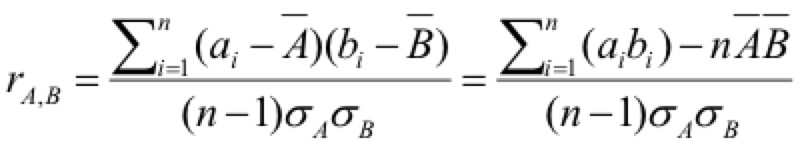
协方差分析:针对数值型数据
协方差:
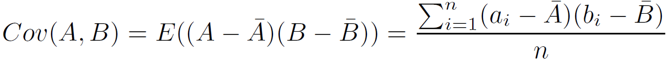

协相关系数(correlation coefficient:):
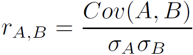
协方差为正,说明 A B 趋向于一起改变,A 大于期望的时候,B 也很可能大于它的期望
协方差为负,说明当一个属性小于它的期望,另一个则趋向于比期望更大
协方差为 0,说明两者独立,因为$E(A · B) = E(A)·E(B)$
数据简化(reduction)
降低维度(Dimensionality Reduction)
动机:维数灾难,当维度增加,数据变得稀疏,
方法:
小波变换(wavelet transforms)
将一个信号分解为不同频率的子带,保留数据对象之间的相对距离,只保留一小部分小波系数最强的信息,和傅立叶变换类似,但空间局部性更好,有助于保留局部细节
为什么选择小波变换
有效移除离群值,多分辨率(在不同缩放率下都可以检测任意形状的聚类),高效(时间复杂度 O(N)),但只适用于低维数据
PCA 主成分分析
找出 k 个最能代表数据的 n 维正交向量(k<=n),也就是找到一个投影能够捕捉到数据中最主要的变换。
- 先标准化输入数据,使得所有属性都投影到同一区间。
- 计算 K 个标准正交向量,这些向量作为规范化输入数据的基,称为主成分。输入数据即为主成分的线性组合
- 对于主成分,按照重要程度或者强度进行排序
- 去掉排序靠后的,不重要的,方差较小的那些正交向量
属性子集选择(attribute subset selection)
通过删除不相关或者冗余的属性来减少数据量。
启发式搜索(贪心算法),属性的好坏,可以用统计显著性检验来确定
- 逐步选择:每次从属性集里选出一个最好的属性,添加到目标集合中
- 逐步删除:每次从属性集中删除一个最差的属性
两者结合:每次都选出一个最好属性,并删除一个最差的
简化数量(Numerosity Reduction)
参数化方法
假设数据会符合某些模型,这样就可以只记录模型参数,忽略数据(x,y 表示数值属性)
- 线性回归:简单直线($y=wx+b$)
- 多元回归:用多个自变量的线性函数对因变量 Y 进行建模($y=b_0+b_1x_1+b_2x_2+…+b_kx_k$)
- 对数线性模型:对于离散属性值,可以用对数线性模型,基于维组合的一个较小子集,估计多维空间中每个点的概率。
非参数化方法
未假设模型的存在
- 直方图:等宽分割(宽度接近)和等频分割(高度接近)
- 聚类
- 采样
- 无放回简单随机采样
- 有放回简单随机采样
- 分层抽样(stratified sampleing):分割数据集。对倾斜数据比较有效
- 数据立方聚集
数据压缩(Data Compression)
- 字符串压缩
- 音频/视频压缩
数据变换和数据离散化
数据变换
光滑(去除噪声)
属性构造( 由已有的属性构造出新属性添加到属性集中)
聚集(汇总)
规范化(标准化)
min-max,标准化到[new_min, new_max]
$v’=\frac{v-min}{max-min}*(new_max-new_min)+new_min$
z-score
$v’=\frac{v-\mu}{\sigma}$
小数定标 decimal scaling
$v’=\frac{v}{10^j}$,其中 j 是使得 v’最大绝对值小于 1 的最小的整数
离散化
离散化
- 分箱:无监督,自顶向下分裂,指定箱的个数;容易受离群值影响;有等宽和等深频
- 直方图:无监督,自顶向下分裂,等宽/等频
- 聚类:无监督,自顶向下分裂/自下向上合并
- 决策树:有监督,自顶向下分裂。
- 相关性分析。有监督,自下向上合并
概念分层
通过用户或专家,显式的说明部分或者所有的属性层次序列
通过显示数据分组,说明分层结构的一部分,比如定义{浙江,江苏,福建}属于华东地区
自动根据每个属性的不同值个数产生概念分层
4. 数据仓库和联机分析处理
5. 数据立方技术
6. 挖掘频繁模式、关联和相关性
基本概念
动机:找到数据的内在规律
项集(itemset)
事务(transaction),为一个非空项集
频度(frequency),
关联规则(association rules),X=>Y,X,Y 是两个不相交的非空项集。
强关联规则:支持度和置信度都高于阈值
支持度(support):包含$X \cup Y$的事务的出现概率
置信度(confidence):包含 X 的事务同时也包含 Y 的概率,P(Y|X)
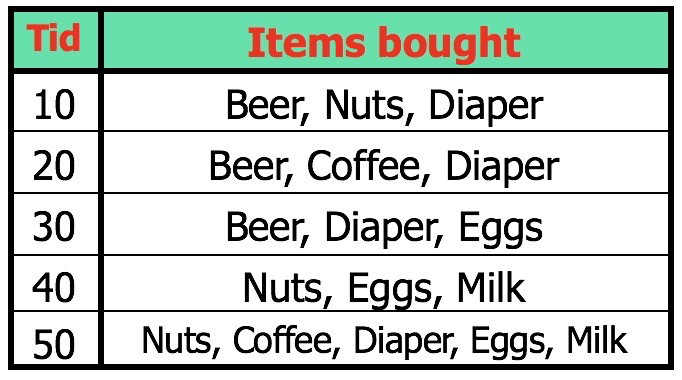
$support(Beer \Rightarrow Diaper)=count(10,20,30) / 5 = 60\%, confidence(Beer \Rightarrow Diaper)=count(10,20,30) / count(10,20,30) = 100\%$
$support(Diaper \Rightarrow Beer)=count(10,20,30) / 5 = 60\%, confidence(Diaper \Rightarrow Beer)=count(10,20,30) / count(10,20,30,50) = 75\%$
因为长项集的子项集组合过多,比如包含 100 项的相机,它的子集组合就有$2^{100}-1$个。故而把问题转换成挖掘其中的闭频繁项集和极大频繁项集:
- closed pattern:如果不存在 X 的真超项集 Y,使得 Y 和 X 在数据集 D 中有着相同的频度,那么称 X 为闭的(closed)
- Max-Patterns:如果 X 是频繁的,且不存在 X 的超项集 Y,并且 Y 是频繁的
时间复杂度:最坏情况$M^N$,M 是不同的项个数,N 是事务的最大长度
#
Apriori 算法:
基于一个先验性质,频繁项集的所有非空子集也一定是频繁的,反而言之,如果一个项集是不频繁的,那么它的任何超集也都不用再进行验证。
- 第一次生成一项集,排除里面支持度小于阈值的项集。
- 根据上一次生成的项集,形成 N+1 项集
- 排除 N+1 项集中,支持度小于阈值的项集,重复上一步,直到所有项集的支持度都低于阈值
案例:

提高 Apriori 算法:
- 问题:多次扫描数据库中的事务,庞杂的候选项,计数候选项支持度的开销大
- 解决:
- 划分(partition):只需要两次扫描数据库。第一次,将数据库 D 中的事务,划分成 n 个非重叠分区,计算每个分区的局部最小支持度计数阈值(min_sup * 分区事务个数)。若项集超过这个局部最小支持度计数,那么认为这个项集是局部频繁项集。全局的频繁项集一定出现在局部频繁项集中,故而将局部频繁项集作为 D 的候选项集;第二次,再次扫描 D,评估候选项集的实际支持度,删除低于阈值的项集。
- 散列(hash,DHP):利用散列哈希,如果哈希结束后,桶中的项集个数比阈值还小,那么这个桶中的项集就一定会被淘汰。而桶中项集个数大于阈值,也不一定就是频繁项集。
- 采样(sampling):牺牲精度换取可行性。利用 D 的一个采样 S,找出 S 中的频繁项集(故而阈值也会重新计算,此时的频繁是相对 S 的频繁),但 S 中的频繁项集并不一定是 D 中的频繁项集,会有丢失。故而要用低于最小支持度的阈值来搜索 S,从而提高精度。
- 动态项集计数(DIC)
模式增长方法(Pattern-Growth Approach)
构建 fp tree:
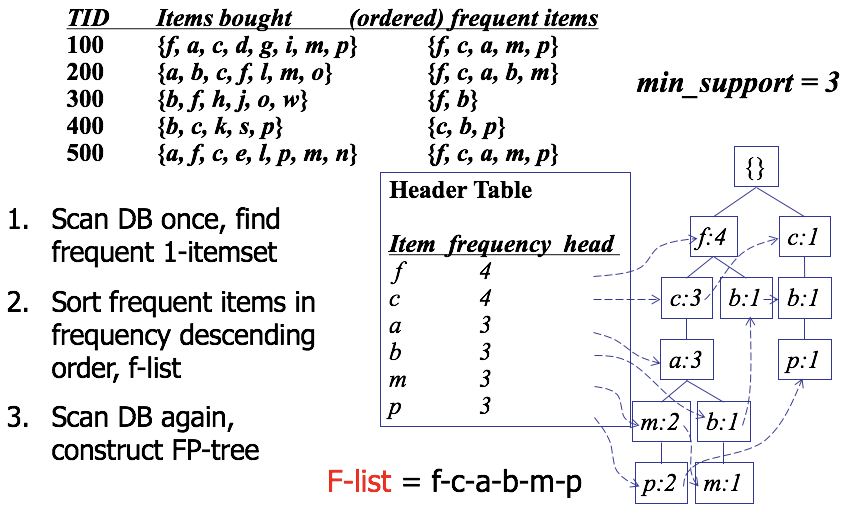
条件模式基(conditional pattern bases)
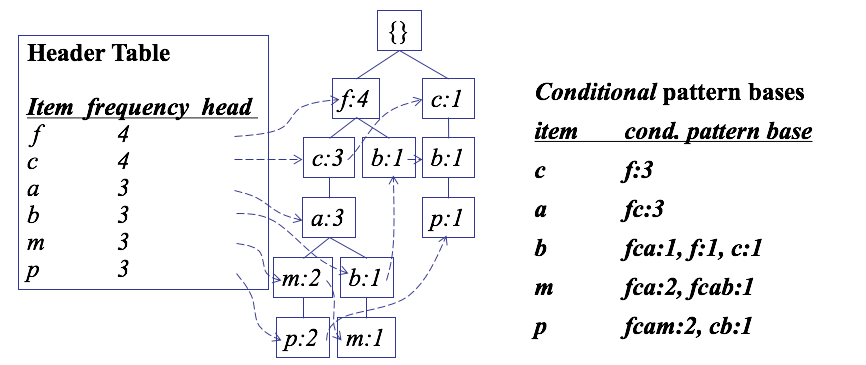
寻找条件模式树(conditional FP-tree,类似于寻找最长公共子序列)
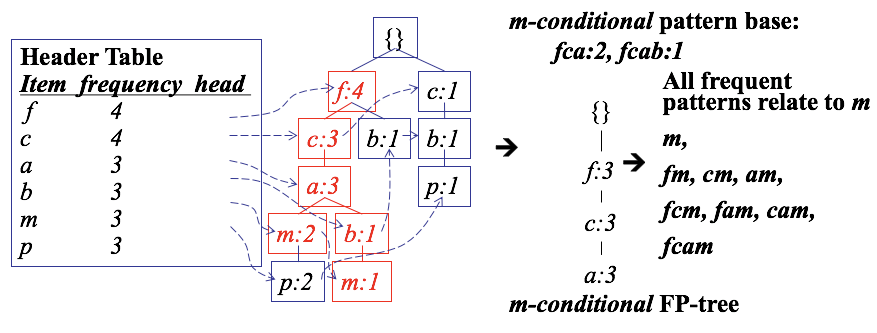
简化,前缀可以被简化成一个节点
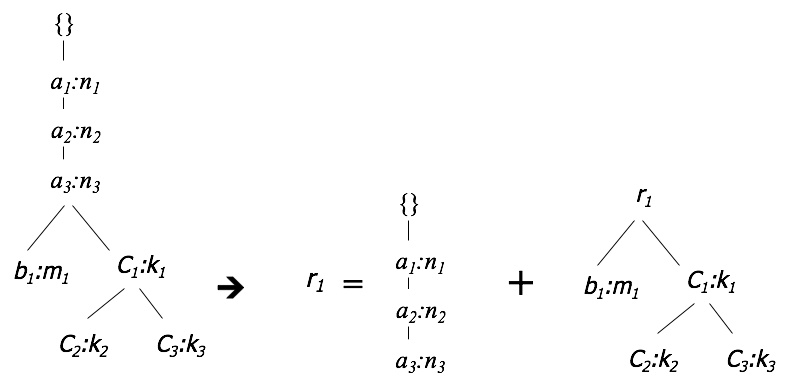
fp-tree 的优势
- 完全性(completeness):包含了 fp mining 需要的所有信息,不拆分任何一个事务的长 pattern
- 紧密型(compactness):去除了无关信息(非频繁的项被省去);高频项被放在前面;不会比初始数据库更大
挖掘方法
- 对每个频繁项,构造它的条件模式基(conditional pattern-base),进而构造它的条件频繁模式树(conditional FP-tree)
- 对每个 conditional FP-tree,重复以上步骤
- 直到 FP-tree 是空的,或者只有一条路径(单一路径的所有子路径,组成了频繁模式)
分割投影
为了让 fp-tree 能放进主存,需要将数据库划分成投影数据库的集合。比如 4 图中,就可以先分成两个以 r1 为前缀项集的投影数据库$\{b1\},\{ \{c1,c2\},\{c1,c3\}\}$
用等价类变换(ECLAT)进行垂直数据格式挖掘
前面的方法都是 TID 项集格式的挖掘方式,这种数据格式称为水平数据格式;而垂直数据格式刚好是它的一个转置。$t(X)= {T1,T2,T3}, t(XY) = {T1, T3}$
加速:比如上方,$Diffset(XY,X)={T2}$,这样就不用记录$t(XY)$的两个项,而只要存储差集的一个项就行了。
挖掘闭频繁模式和极大模式
挖掘闭模式
- 项合并:如果包含频繁项集$X$的事务都包含$Y$,且不包含$Y$的任何真超集,那么$X \cup Y$形成一个闭频繁项集,并且可以不再搜索包含$X$且不包含$Y$的任何项集。
- 子项集剪枝:如果 X 是一个已发现的闭频繁项集 Y 的真子集,且$support_count(X)=support_count(Y)$(说明,X 没有单独出现在任何事务中),那么 X 和 X 的子集都不可能是闭频繁项集
- 项跳过:在头表不同层,某个局部频繁项都有着一样的 support,那么这一项就可以从头表中删除
挖掘极大模式
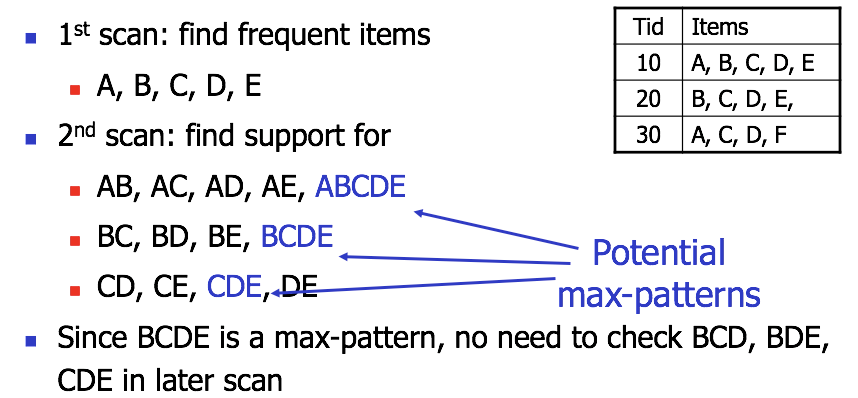
找出 interesting pattern
强关联规则并不一定准确。需要其他度量
correlations(相关性)。
提升度 lift
假如 A 项集和 B 项集的出现是独立事件,那么$P(A \cup B) = P(A)P(B)$;否则,两者相互依赖(dependent)和相关(correlated),可以通过提升度(lift)来表示
$lift(A, B) = \frac{P(A \cup B)}{P(A)P(B)}=\frac{P(B|A)}{P(B)}$
如果提升度小于 1,说明发生 A 时发生 B 的概率,比光是发生 B 的概率要小,A 和 B 负相关;
如果提升度大于 1,说明发生 A 时发生 B 的概率,比光是发生 B 的概率还大,A 和 B 正相关;
如果提升度等于 1,说明发生 A 时发生 B 的概率,和光是发生 B 的概率一致,说明两者无关独立。
卡方$\chi^2$
不平衡比(Imbalance Ratio)
$IR(A, B) = \frac{|sup(A)-sup(B)|}{sup(A)+sup(B)-sup(A \cup B)}$
分子是支持度之差的绝对值;分母是包含 A 或 B 的事务个数。越大越不平衡。
7. 高级模式挖掘
8. 分类
预测问题包括分类和数值预测。
分类:一个两步过程
- 模型建构
- 每个样本都假设属于一个预定义的类
- 模型可能表现为:分类规则,决策树或者数学公式
- 模型使用
- 评价模型精确程度
- 假如精确度可接受,那么就可以用来标记新数据
- 监督学习和无监督学习
- 监督学习:训练数据是有标记的
- 无监督学习:训练数据无标记,目标是进行聚类
决策树归纳
决策树的构建算法:自顶向下的递归分治算法
- 一开始所有训练样本都在根节点上,所有的属性都是有类别的(假如是连续的,需要提前离散化)
- 基于参数中给定的分裂准则,用选定的属性对样本进行划分,不断迭代
- 直到满足以下任一条件:
- 给定节点中的所有样本都是同一类的
- 没有剩余的属性可以被用来做进一步分割
- 没有剩余的样本了
决策树构建中的分裂准则
信息增益(Information Gain)
选择具有最高信息增益的属性作为节点 N 的分裂属性
对 D 中的元组进行分类所需要的期望信息,也被称为 D 的熵:
$Info(D)=-\sum p_ilog_2(p_i)$
$p_i$是$D$中任意元组属于类$C_i$的概率(非 0)
利用某个属性对 D 进行分区,得到的分区不一定是准确的分类,所以需要计算,要得到准确的分类,我们还需要多少信息:
$Info_A(D)=\sum \frac{|D_j|}{|D|} \times Info(D_j)$
其中$\frac{|D_j|}{|D|}$充当第 j 个分区的权重。$Info_A(D)$是基于 A 划分 D 所需要的期望信息,所需的期望信息越小,分区的纯度越高。
信息增益:
$Gain(A)=Info(D)-Info_A(D)$
选择最高信息增益的属性作为分裂属性,也就是说选择$Info_A(D)$最小。
计算连续值得的信息增益
A 的值进行递增序排序,每对相邻的中值作为一个可能的分裂点($(a_i+a_{i+1})/2$),对于 A 的给定的 v 个值,则需要计算 v-1 个可能的划分。
对每个分裂点计算$Info_A(D)$,对每个分裂点,分区个数是 2,选出最小期望信息需求的点作为分裂点。
增益率
$GainRate(A) = \frac{Gain(A)}{splitInfo_A(D)}$
其中,
$splitInfo_A(D)=-\sum \frac{|D_j|}{|D|} \times log_2(\frac{|D_j|}{|D|})$
基尼指数(Gini index),针对二元分裂
基尼指数,度量 D 的数据分区的不纯度:
$Gini(D) = 1 - \sum p_i^2$
利用属性 A,将 D 划分为两个分区,从而得到的基尼指数:
$Gini_A(D)=\frac{|D_1}{|D|}Gini(D_1)+\frac{|D_2}{|D|}Gini(D_2)$
基尼指数下降:
$\Delta Gini(A)=Gini(D)-Gini_A(D)$
过拟合和剪枝
- 因为噪声跟离群点的关系,有许多分支反映了训练数据中的一场,需要进行剪枝来处理这种过拟合的问题。
- 先剪枝和后剪枝
- 先剪枝(prepruning),通过提前停止树的创建来剪枝
- 后剪枝(postpruning),删除节点的分支而用叶节点代替
大数据库的分类
可伸缩的决策树算法,RainForest:
AVG-set:在每个节点上,对每个属性都维护一个 AVC-set。
AVC-group:节点上的所有 AVC-set 的集合。
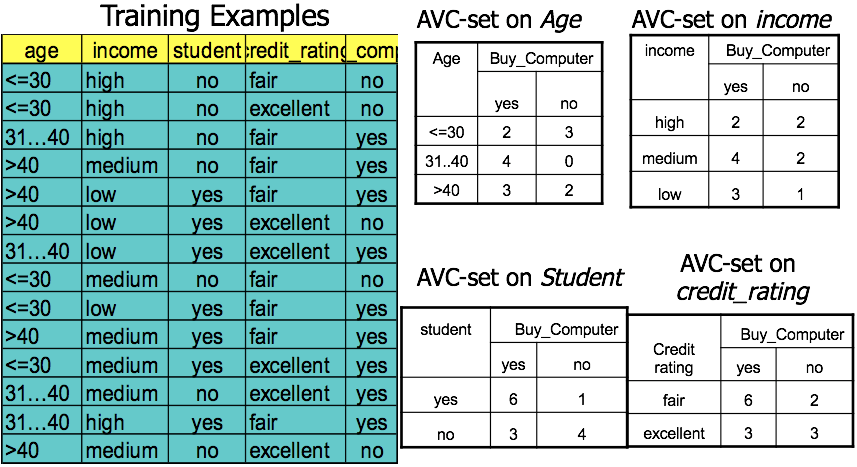
贝叶斯分类方法
贝叶斯定理
先验概率,$P(H)$是 H 的先验概率
后验概率:$P(H|X)$是在条件 X 下,H 的后验概率
贝叶斯定理:
$P(H|X)=\frac{P(X|H)P(H)}{P(X)}$
朴素贝叶斯分类
最大化$P(C_i|X)$:假定一个 tuple 用一个 n 维属性向量$X=\{x_1,x_2,…x_n\}$表示,且假定有 m 个类,那么配件单贝叶斯分类法中,预测$X$属于$C_i$的概率为:$P(C_i|X)$,只要找到这个最大值对应的$C_i$即可。
最大化$P(X|C_i)$:而根据贝叶斯公式,只要找到$P(X|C_i)P(C_i)$的最大值即可。加入类的先验概率未知,我们通常假设所有类的先验概率一致,于是我们只要找到$P(X|C_i)$的最大值即可
假设$X$的各个属性之间相互独立,不存在依赖关系,那么
$P(X|C_i)=\prod P(x_k|C_i)$
如果属性$x_k$是分类属性,那么概率即为训练集中属性值为$x_k$,且属于$C_i$的 tuple 在$C_i$中的比例
如果属性是连续值,一般假设属性服从高斯分布。
$P(x_k|C_i)=g(x_k,\mu_{C_i},\sigma_{C_i})$
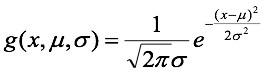
example

关于 0 概率:拉普拉斯校准
假设训练集很大,对每个计数都加 1,也不会对概率产生太大变化,从而避免 0 概率
优缺点
- 优点:容易实现,在大部分情况下结果不错
- 缺点:基于分类条件独立假设,可以用贝叶斯信任网络来解决这个问题
模型评估与选择
混淆矩阵:对于给定 m 个类,混淆矩阵至少是一个 m*m 的表。以下是一个 2*2 的混淆矩阵,纵向是实际分类,横向是预测分类。

- 准确率:$accuracy=(TP+TN)/(P+N)$
- 错误率:$error rate=(FP+FN)/(P+N)$
- 有些数据是不平衡的,比如在癌症检测,显然 cancer=yes 的元组才是我们关注的,于是有了以下两个度量:
- 灵敏性(正确识别的正元组的比例):$sensitivity=TP/P$,反映了识别正例的能力
- 特效性(正确识别的负元组的比例):$specificity=TN/N$,反映了识别反例的能力
- 精度(正确识别的正元组在预测为正元组中的比例):$precision=(TP)/(TP+FP)$
- 召回率:$recall=TP/P$,其实也就是灵敏性
- $F$度量:$F=(2 \times precision \times recall)/(precision+recall)$
- $F_\beta$度量:$F_\beta=((1+\beta^2) \times precision \times recall)/(\beta^2 \times precision+recall)$
保持方法和随机二次抽样
- 保持方法(holdout):将数据随机的分成训练集跟检验集(通常 2/3 作为训练集)
- 随机二次抽样(random subsampling):将保持方法重复 k 次,结果取平均值。
交叉验证(cross-validation)
- k 折交叉验证(k-fold cross-validation),将数据随机分成 k 个相互不相交的子集(折),进行 k 次训练和检验。其中第 i 次迭代,用分区 i 作为检验集而用其余的作为训练集。准确率计算是用 k 次迭代的总数进行计算。
自助法(bootstrap)
在小数据集下比较好。
$.632$自助法:对于给定的包含 d 个元组的数据集,有放回抽样 d 次,产生 d 个样本的自主样本集或训练集,其余作为验证。平均情况下,63.2%的数据会被用于训练。
准确率计算:
$Acc(M)=\sum(0.632 \times Acc(M_i)_{test_set} + 0.368 \times Acc(M_i)_{train_set})$
$Acc(M_i)_{test_set}$是对于检验集 i 的准确率,$Acc(M_i)_{train_set})$是对于源数据的准确率
选择模型的标准:
- 准确率
- 速度
- 鲁棒性
- 可扩展性(对于大数据库的高效性)
- 可解释性
提高分类准确率
- 装袋(bagging):对于不同的训练集 Di(每个训练集都是一个自助样本)训练的分类模型 Mi。为了对一个未知元组 X 进行分类,每个分类器 Mi 都会返回它的预测结果,算作投票中的一票,统计最终的票,将最高的得票赋予 X。
- 提升(boosting):迭代学习。初始所有训练集的元组权重都一致,每一轮迭代,提升上一次测试中出错的元组的权重,降低正确的元组的权重。
- 随机森林(random forest)
9. 高级分类方法
惰性学习法
k-最近邻分类
10. 聚类
聚类质量
- 高类内相似度,低类外相似度
- 聚类质量依赖于:相似度度量;聚类的实现;能够发掘隐藏 pattern 的能力
- 聚类质量的度量方法:相异度/相似度矩阵
- 聚类分析需要考量的因素:
- 划分准则:单层划分和多层划分(互相之间有层级关系)
- 簇的分离性:互斥(一个客户只能属于一个组)和不互斥(一个文档可能有多个主题)
- 相似度度量:基于距离和基于连通性
- 聚类空间
- 可伸缩性
- 处理不同类型属性的能力
- 有约束条件的聚类
主要聚类方法
划分方法
- 将数据划分成 k 个分区,保证每个分区最少有一个对象;例如 k-means,k-medoids,CLARANS
- 发现球形互斥的簇
- 对中小规模数据集有效
层次方法
- 凝聚或者分裂的方法。层次聚类方法可以是基于距离或者密度和连通性的。
- 无法纠正错误的合并或划分
基于密度的方法
基于对象之间的距离进行聚类,只能发现球状簇。主要思想:只要“邻域”中的密度超过某个阈值,就继续增长。对于给定簇中的每个数据点,在给定半径的邻域中至少包含最少数目的点。
基于网格的方法
用网格化的方法把对象空间量化为有限个单元。
划分方法
一种度量簇质量的方法:
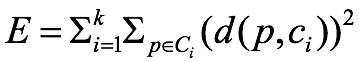
$c_i$是簇$C_i$的代表(形心)
k-means:局部最优,但不一定收敛到全局最优
将簇的形心定义为簇内点的均值。
- 初始选取 k 个点,每个点代表一个簇的初始均值或中心。
- 其余点根据欧氏距离,分配给距离最近的簇。
- 更新迭代簇内均值,再分配。
直到不再变化。
优点是高效;缺点是只在连续 n 维空间中有效,需要提前确定 k,对噪声和离群值敏感,无法处理非凸形状的数据
k-medoids
将簇的形心定义为簇内某个实际的点。
- 初始选取 k 个点,每个点代表一个簇的初始均值或中心。
- 其余点根据欧氏距离,分配给距离最近的簇。
- 随机选择一个非代表对象$O_{random}$代替$O_j$,观察绝对误差标准是否降低
- 如果降低,那么说明应该进行替换,并且重新形成簇
直到不再变化
其中,绝对误差标准(absolute-erro criterion)的计算方法:如上。
层次方法
基于密度的方法
主要特点:
- 可以发现任意形状的簇
- 能应对噪声
- 只扫描一遍
- 需要密度参数作为终止条件
参数和基本概念:
Eps:邻域的最大半径(确定领域大小)
MinPts:邻域最大半径内的最小点数量(确定邻域最大密度)
核心对象(core object):eps 邻域内至少包含 MinPts 个对象(MinPts 由参数给定)
直接密度可达(directly density-reachable):p 在 q 的 eps 邻域内,说明 p 是 q 直接密度可达的
密度可达的(Density-reachable):存在对象链 p1,…,pn,后一个是前一个直接密度可达的,那么说明 pn 是 p1 密度可达的;密度可达并不是一个等价关系,只有当 p1,pn 都是核心对象时,才一定保证可逆。
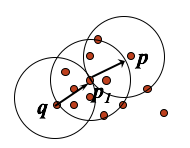
密度相连的(Density-connected):存在 p1,p2,q,p1 和 q 以及 p2 和 q 都是密度可达的,那么 p1 和 p2 是密度相连的。密度相连是等价关系。
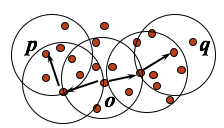
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)
对每个核心对象,将它的所有密度可达的(但未被访问过的)对象添加到自身集合中作为它的簇。
未被添加的点,就是噪声
基于网格的方法
聚类评估
评估聚类趋势(assessing clustering tendency)
只有对有非随机结构的数据集进行聚类,才有可能产生有意义的聚类。所以聚类要求数据的非均匀分布。
霍普金斯统计量(Hopkins Statistic)

确定簇数量(determine the number of clusters)
测定聚类质量