在做到leetcode 287 题时，遇到了这个问题：

Given an array _nums_ containing _n_ + 1 integers where each integer is between 1 and _n_ (inclusive), prove that at least one duplicate number must exist. Assume that there is only one duplicate number, find the duplicate one.

Example 1:

1
2
Input: [1,3,4,2,2]
Output: 2

Example 2:

1
2
Input: [3,1,3,4,2]
Output: 3

Note:

  1. You must not modify the array (assume the array is read only).
  2. You must use only constant, _O_(1) extra space.
  3. Your runtime complexity should be less than _O_(n2).
  4. There is only one duplicate number in the array, but it could be repeated more than once.

看到了快慢指针这个解，最快能达到$O(N)$的时间复杂度，于是详细分析了一下这题。

一般会用两个指针一起遍历数组，快指针每次移动 2 步，慢指针每次移动 1 步。就跟跑步一样，假如在这个链表当中存在环的话，就快指针总是会追上慢指针，这个时候刚好超过慢指针$n$圈，并且快指针跑过的距离刚好是慢指针的两倍。

我们看图，慢指针从 A 开始，在 B 点进入了环中，经过$n$轮后，在 C 点和快指针相遇了。假设 AB 的长度是$a$，$BC$的长度是$b$，B 的循环的长度是$c$，那么从 B 点走到 C 点需要经过$c-b$

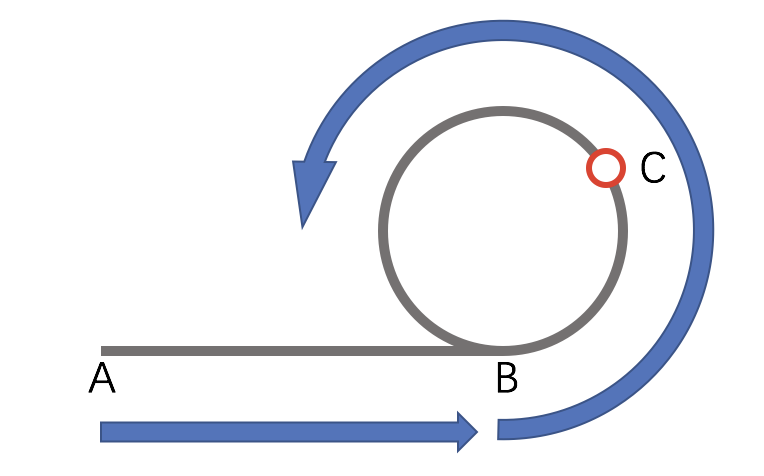
此时，慢指针走过的距离是$a+nc+b​$，快指针假设是$a+Nc+​$b，因为它们速度差是 2 倍，所以：

其中，$x$可以是任意大小。

我们来解释一下上述结论：

  1. $a+xc$的意义就是，从 A 点出发，在 B 点进入循环，并经过$x$圈又回到 B 点
  2. $(N-2n-1+x)c+c-b$的意思则是：从 C 点继续向后走，走过$c-b$的长度后，回到 B 点，又经过$(N-2n-1+x)$圈回到 B 点
  3. 上述两者相同的意思是，此时指针又会共同指向 B 点，那么我们就找到了进入循环的点。

在题中，我们可以将数组看成一个链表，比如[1,3,4,2,2]可以看成一个$1\rightarrow3\rightarrow2\rightarrow4\rightarrow2\cdots$的链表（数组元素表示该元素指向的下一个元素的下标，如果看不懂，读代码就好）。然后我们就可以发现链表会在重复值那里进入循环，于是找到进入循环的点的时候，就可以找到重复值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
 * @param {number[]} nums
 * @return {number}
 */
var findDuplicate = function (nums) {
    let slow = nums[0],
        fast = nums[nums[0]],
        t = nums[0]
    while (slow != fast) {
        slow = nums[slow]
        fast = nums[nums[fast]]
    }
    slow = nums[slow]
    while (slow != t) {
        slow = nums[slow]
        t = nums[t]
    }
    return slow
}

关于快慢指针的应用

  • 单向链表是否存在循环：只要快指针和慢指针相遇，则一定存在环
  • 寻找无环链表的中位数：当快指针指向链尾时，慢指针指向链中
  • 找链表中环的入口点：如上所述
  • 两个单向无环链表是否相交：将其中一个链表首尾相连，另一个链表开始进行快慢指针遍历，就转化成了第一个问题