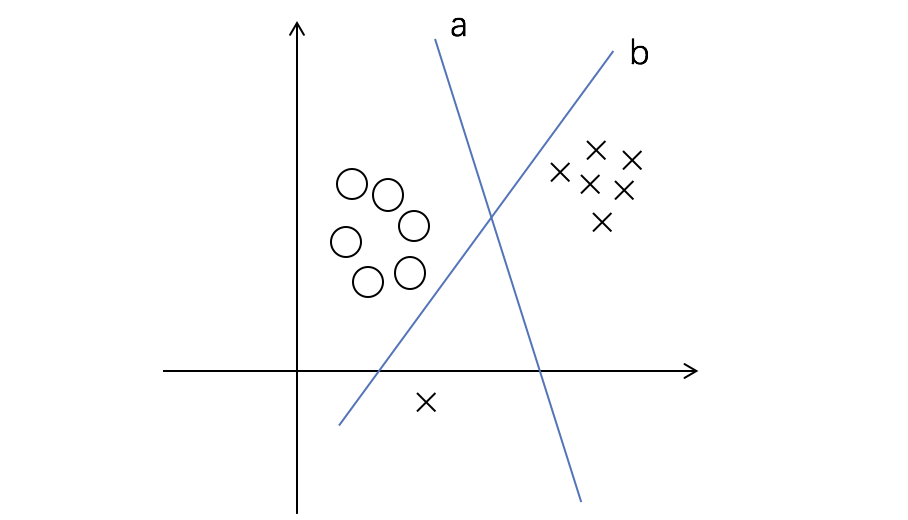
当数据中存在异常点时,比如上述的情况,导致原先可以用直线 a 分割的数据现在不得不用 b 来进行,以保证完美的分割。由此我们引出了非线性决策边界(_non-linear decision boundaries_)来解决这样的问题。
观察原 SVM 问题的目标:
我们为原公式增加惩罚项,对不同的数据点增加不同的惩罚,使得所有样本能够更好地分割:
使得
注意到,我们之前认为$ y^{(i)} \cdot (w^T \cdot x^{(i)}+b) \geq 1 $是分类正确的,在这里我们允许一部分样本小于 1,也就是说明我们允许了一部分样本分类错误。
构建拉格朗日算子:
对偶:
跟原先的 SVM 问题的唯一区别在于其限制条件为:
其收敛条件:
对于大部分数据点:
对于异常点:
对于最近点:
坐标上升法(Coordinate Ascent)
考虑优化问题:
不考虑约束条件,
重复 {
For i = 1 to m:
} 直到收敛;
这个算法,可以认为是执行了以下这个过程(以 m=2 为例):
顺序最小优化算法(Sequential minimal optimization, SMO)
顺序最小优化算法的基本理念就是在坐标上升法的基础上,改成一次性优化其中两个$\alpha$,而固定其他的$m-2$个$\alpha$。
假如我们更新$\alpha_1, \alpha_2$:
因为在之前我们提到:
于是有:
那么
在非线性决策边界优化问题中,其实$W$是一个关于$\alpha_i$的二次函数,固定其他$\alpha$之后,$W$函数就可以被简化为:
很容易就能求解。