Simultaneous Matrix Orderings for Graph Collections

论文：Simultaneous Matrix Orderings for Graph Collections

作者：Nathan van Beusekom, Wouter Meulemans, and Bettina Speckmann

发表：VIS 2021

单位：荷兰埃因霍温理工大学（Eindhoven University of Technology）

一般而言，图数据并不会单独存在，而是以一个集合的形式存在。对这些图进行矩阵可视化时，需要考虑如何同时对一个集合内所有图数据对应的矩阵进行重排序。现有解决方法是将这些矩阵聚合成一个权重矩阵再进行统一排序。然而这种聚合会丢失信息。本文的解决方案是：先提出使用Moran’s I的度量指标来衡量矩阵中的连续块，其次针对这个指标改进了两种现有的算法，使得他们能够应用于一整个集合的图数据。最后，利用Moran’s I指标，作者对比了传统集合图数据矩阵可视化重排序算法和他们提出的算法。

论文链接：https://arxiv.org/pdf/2109.12050.pdf

报告链接：Slides

节点链接图和矩阵是可视化图数据的两种重要方式。其中矩阵被认为对于执行一些低层级的分析任务很有用（比如看节点之间的连通性）。在合适的行列排序下，矩阵也可以用于显示一些图数据的局部结构。然而，这里还有两个具有挑战的问题：1）正式定义排序的质量；2）自动计算高质量的排序。

图数据集合对应的矩阵集合如何排序？虽然已经有很多工作已经尝试解决了这两个问题，但是它们往往解决的是单个矩阵的排序问题。在通常情况下，矩阵，或者说其对应的图数据并不是独立出现的，而是以集合的形式出现（比如动态图）。一个集合的矩阵需要统一的排序，这样不同的矩阵之间才能进行比较，但与此同时，又需要能够让每个矩阵能够表达其蕴含的结构。

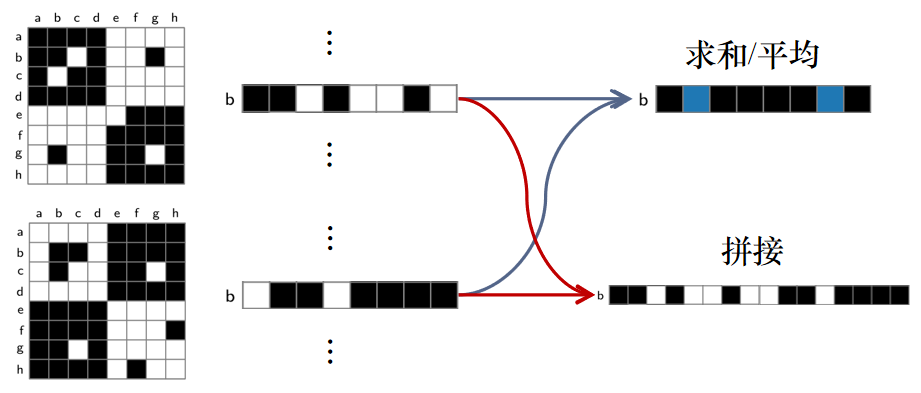
现有的算法可以大致分成两种：第一种选择一个矩阵进行排序，然后应用到其余矩阵；第二种则是将一个矩阵的集合合并成一个权重矩阵，然后对合并后的矩阵进行排序（下图所示）。这两种方式都存在信息损失的问题，第一种无法兼顾其余矩阵，第二种合并后则丢失了每个矩阵各自的拓扑信息。

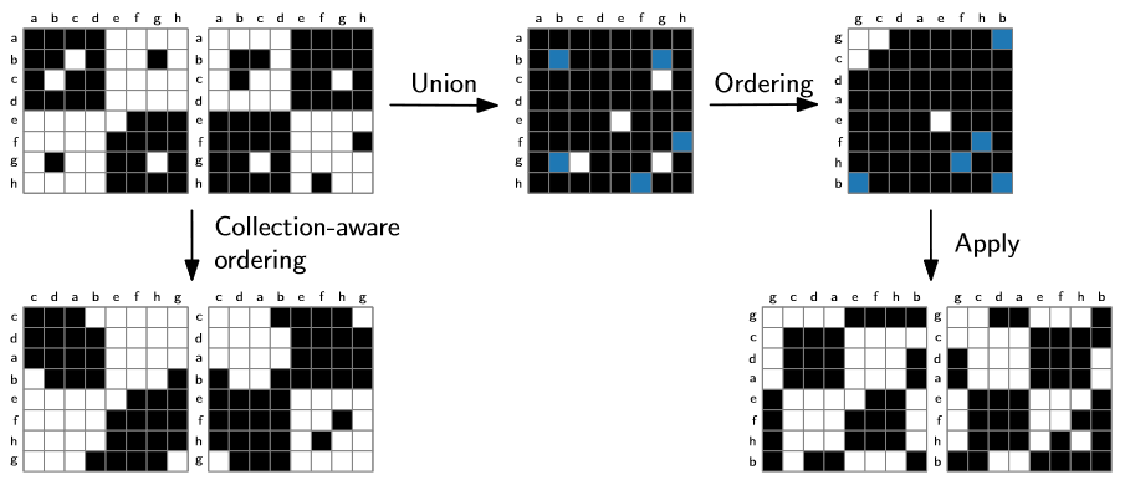
作者提出的一种collection-aware的方法，能够同时计算一整个集合的矩阵的排序，而防止信息丢失。作者最后在两类较为流行的矩阵排序算法，叶排序算法（leaf order）和质心算法（barycenter）上说明了方法的有效性。

矩阵的排序质量。在解决计算排序的问题后，作者还关注到以前对于排序质量的定义方法，包括bandwidth，profile，linear arrangement等度量方法目的都是为了衡量矩阵单元格（也就是图数据中的边）离对角线有多远。但是，在一些重要的矩阵模式中，比如完全二部图（bi-cliques）或者星型图（star）中，一些边所对应的单元格都是远离对角线的。而它们的共同特性则表现在连通性上，也就是一些重要的模式往往是连通的，矩阵中的黑色单元格会被聚合。所以，作者提出了使用莫兰指数，一种空间自相关指标，来衡量矩阵的排序质量。简单而言，这种度量方式会计数矩阵中横向或者竖向出现的黑-黑相邻和白-白相邻，来表示矩阵中出现的块的数量。

文章贡献。本文的贡献可以被概括为两点：1. 一种collection-aware的矩阵集合统一排序的方法；2. 提出了将莫兰指数作为矩阵排序质量度量方法。

最后，作者用定量实验对比了传统集合重排序方法和它们的方法在莫兰指数上的表现。实验证明，collection-aware的方法的确表现更佳。

排序质量度量方法

现有的度量方法主要有三种，几乎都是为了度量矩阵中的黑色单元格到对角线的距离，优化这些度量的好处是可以将黑色单元格聚合到对角线附近，从而在对角线附近形成有意义的模式（主要是block，也就是完全图）。其中Linear Arrangement（LA）度量的是每一行中最远的黑色单元格离对角线的距离之和，Profile（PR）度量的是每一个单元格到对角线的距离之和，Bandwidth（BW）则是整个矩阵中离对角线最远的单元格到对角线的距离。

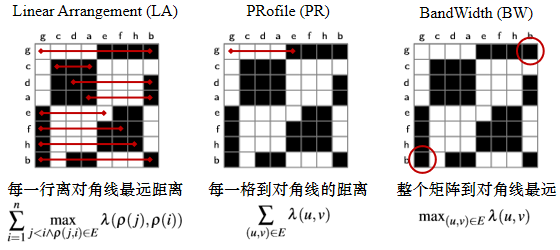
它们存在的问题之一是，以这些度量为目标优化矩阵，只能能凸显对角线块状模式（也即完全图，下图左上角），其余四种常见的模式（下图黑色的矩阵）都无法满足。

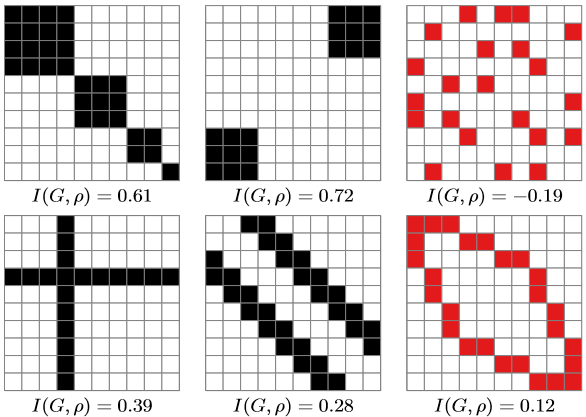
作者发现用单元格之间的邻接关系更容易描述这些有意义的模式。于是作者提出了使用莫兰指数来度量矩阵的排序质量。莫兰指数，1950年由莫兰提出，是一种空间自相关的度量方法，在将这种算法应用于矩阵后，可以简化得到右面的公式，其中$c_{W}(G)$和$c_{B}(G)$都是常数项，与图数据中节点和边的数量有关。$W(G, \rho)$和$B(G, \rho)$则分别统计了白白相连，黑黑相连的数量（如下图所示）。并且，有意义的模式（上图黑色的四个）的莫兰指数会较大，而无意义的模式（上图红色的两个）则会较小。

$$I=\frac{r}{t} \cdot \frac{\sum_{a=1}^{r} \sum_{b=1}^{r} T_{a b}\left(x_{a}-\bar{x}\right)\left(x_{b}-\bar{x}\right)}{\sum_{a=1}^{r}\left(x_{a}-\bar{x}\right)^{2}} \rightarrow I(G, \rho)=c_{B}(G) \cdot B(G, \rho)+c_{W}(G) \cdot W(G, \rho)-1$$

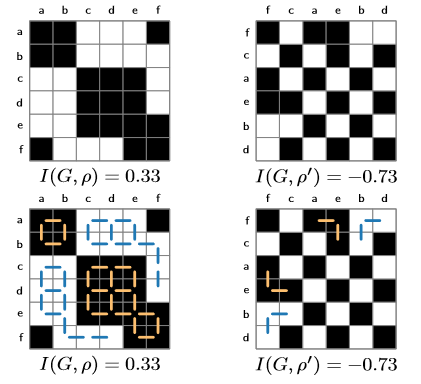
作者进一步推导了如何使用莫兰指数来重排序矩阵。在重排序矩阵的时候，度量矩阵中的两行（也就是两个节点）的相似度比较重要，而莫兰指数也可以用于衡量两行之间的相似度，其做法也同样是计数两行之间黑黑相邻和白白相邻的数量。以往很多基于节点之间相似度的排序算法，都可以将莫兰指数应用于其中。比如叶排序算法leaf order，其目标就是让相邻两行的相似度最大化（也即距离最小化），这实则是一个旅行商问题。所有解决旅行商问题的方法都可以转化为用莫兰指数相似度$\delta_I$作为距离度量。基于这个相似度度量方法（$\delta_I$），作者实现了基于$\delta_I$的最近邻算法，并且用2-OPT算法找到最优的排序。作者提到，对比用$\delta_I$的叶排序算法，能略微提升一些（0.0001）。

矩阵集合排序的同步计算

为了能够对一个集合的矩阵进行重排，作者首先回顾了以往的方法。基于单个矩阵进行排序并应用于其余矩阵的方法并不在作者们的考量范围内，因为这种算法直接忽视了其余所有矩阵的特性。而作者转而考虑了对集合内所有矩阵做合并再排序的算法。作者选取了两类能够对合并后的权重矩阵进行重排序的算法：leaf order叶排序算法以及barycenter质心排序算法。

但以往的算法，最大的问题在于，它们首先将不同的矩阵进行了合并求和，这样就丢失了单个矩阵的拓扑信息，所以在排序过程中会产生质量问题。作者提出的方法可以被简单概括为，将原先的求和机制，改成了拼接机制（如下图红色箭头所示）。这样做的好处是，所有的矩阵信息都会被保留，计算相似度的时候都会再次被用到。

对比实验

为了对比本文提出的矩阵集合重排序算法是否有用，作者对比了传统方法。

算法的设置分三个层面：

1. 矩阵集合的重排序机制：作者对比了 (U) Union 和 (C) Collection-aware
2. 重排序算法：作者使用了 (LO) leaf order 和 (BC) barycenter
3. 算法中的距离度量：作者使用了 欧式距离 $L_2$ 和 莫兰指数 $\delta_I$

这些不同配置的组合下，理论上能够有8种不同的配置，但是因为BC算法并不依赖于距离度量，所以最终只有6种对比算法配置。

数据集则选用了三种不同大小和密度的矩阵集合：

1. 帕金森病患者大脑连通性（96 graphs）
2. 小学学生和老师的社会交往联系（17 graphs）
3. 15年到20年的VIS合作网络（6 graphs）

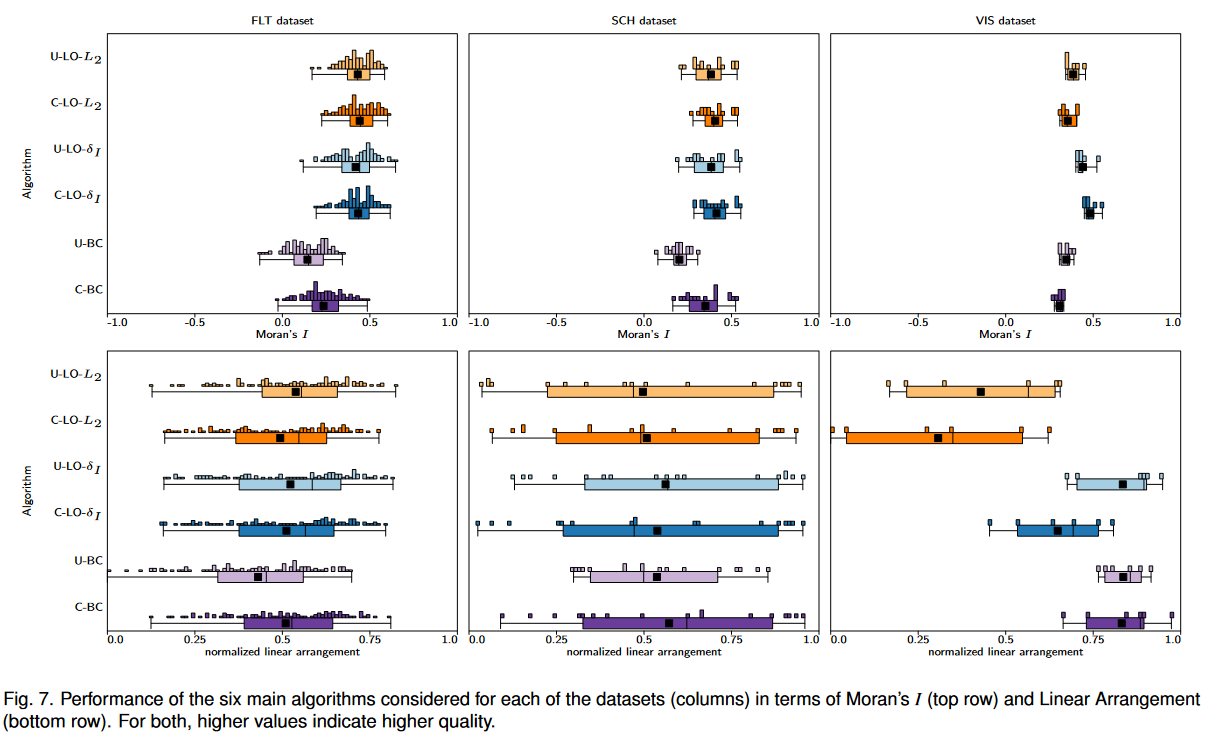
作者对比了这些算法配置在不同数据集上运行后的莫兰指数度量。最终结果绘制如下图：上面一行图是6种算法配置在三个数据集下的莫兰指数。下面一行图则是三个数据集的linear arrangement指标。这种绘制方法，用统计直方图+盒须图的方式展现了分布。

结论：

1. 在叶排序中使用欧式距离时，Collection-aware方法相对于Union方法在中密度矩阵中（SCH）提升最大，因为稀疏和稠密的图数据在合并的过程中信息损失不是很大；
2. 在叶排序中使用莫兰距离时，Collection-aware的方法对于稀疏矩阵也有提升，这说明了在前面的对比中，阻碍稀疏矩阵重排序质量的关键在于其使用了欧式距离；
3. 使用叶排序算法时，使用欧氏距离和莫兰距离的差异在系数矩阵中最明显。
4. 在使用质心算法时，Collection-aware的方法在中密度和高密度矩阵（SCH和FLT）都有提升，但在稀疏矩阵中却下降了；

总体结论：collection-aware的叶排序算法在使用莫兰距离（$\delta_I$）效果最好。